５度圏（ごどけん）

例えば Do を基準にして、完全５度ずつ高めたり低めたりする方法で、音列を作ることができます。このような音の世界のことを「５度圏」といいます。

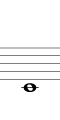
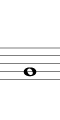
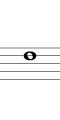
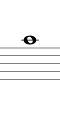
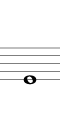
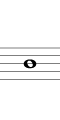
５度で上行する例を下に示します（途中から２オクターブ下げて記します）。結果的にシャープ系となり、Si のシャープ（異名同音で Do） まで進む間に１２平均律のすべての音を通過します。

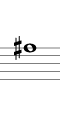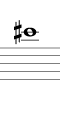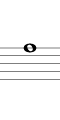
５度で下行する例を下に示します（途中で２オクターブを上げて記します）。結果的にフラット系となり、Re のダブルフラット （異名同音で Do） まで進む間に１２平均律上のすべての音を通過します。

コラム

音程が完全５度上になると、音の周波数は 3/2 倍（1.5倍）になります。完全５度下の周波数は 2/3 倍（0.666...倍）です。このように 3/2 倍（2/3 倍）を重ねていくとすべての音（１２音）を通過して元に戻るなんて・・・　なんともミラクルなお話です。

ところがそんなウマい話でもなく、1.5 倍を積み重ねていって戻ってくるときの音と最初の音との間には、微妙なズレが生じます（これをピタゴラス・コンマという ＝ 半音の 1/4 程度）。

下記の用語で「音律」について調べてみてはいかがでしょうか。きっと勉強になります。

｛　ピタゴラス　純正律　中全音律　平均律　｝

スクールの総合音楽講座「ピタゴラスと平均律とトランペット ／ 曽我部清典著」に詳細が記されています。

https://www.senzoku-online.jp/synthetic_chair/lesson_08-01.html

調号の特徴　１

１）ある調から主音が完全５度 「高く」 なるにつれて、シャープが１つ増えます。

２）ある調から主音が完全５度 「低く」 なるにつれて、フラットが１つ増えます。

ハ長調を基準にすると・・・

　完全５度 「高い」 ト長調は、ハ長調に比べ、シャープが１つ増えてシャープが１つの調号。

　完全５度 「低い」 ヘ長調は、ハ長調に比べ、フラットが１つ増えてフラットが１つの調号。

ト長調 （シャープ１つ） を基準にすると・・・

　完全５度 「高い」 ニ長調は、ト長調に比べ、シャープが１つ増えて　シャープが２つの調号。

　完全５度 「低い」 ハ長調は、ト長調に比べ、シャープが１つ減って　調号なしとなる。

※ もともとシャープが２つある調号でフラットが１つ増えるということは、「シャープが２つと、フラット１つ」になるのではなくて「シャープがフラットで相殺されてシャープが１つ減る」ということになります。